Влияние концентрации полимера

Смешение линейного или разветвленного полимера с низкомолекулярной жидкостью может привести либо к растворению, либо к образованию коллоидной системы – в зависимости от степени дисперсности. При достижении молекулярной степени дисперсности формируются системы истинных растворов, для которых характерны самопроизвольность образования, равновесность, гомогенность, стабильность.

Системы полимер - растворитель, концентрация полимера в которых такова, что взаимодействием между растворенными макромолекулами можно пренебречь, называются разбавленными растворами. Концентрационной границей является величина [h]-1. Макромолекулы в разбавленном растворе представляют собой более или менее анизотропные по форме статистические клубки, способные удерживать в результате сольватации или иммобилизации некоторое количество молекул растворителя. Свободное движение таких молекулярных клубков может быть уподоблено движению сферической частицы, радиус которой соответствует большой полуоси гипотетического эллипсоида вращения, а объем ее равен объему статистического клубка. Вязкость таких растворов описывается уравнением Эйнштейна. Однако асимметрия молекулярных клубков является причиной проявления аномалии вязкостных свойств даже в разбавленных растворах синтетических и природных полимеров вследствие ориентации таких частиц в потоке при достаточно больших t, а также из-за гидродинамического взаимодействия. При небольших и средних t разбавленные растворы полимеров являются ньютоновскими жидкостями.

Растворы полимеров, в которых отсутствует линейность концентрационной зависимости вязкости, называются концентрированными.

Следует отметить неопределенность понятия «концентрированный раствор полимера», тем более что граничное условие Ск » [h]-1 тоже приблизительно. В зависимости от термодинамической гибкости макромолекул область перехода от разбавленных к концентрированным растворам составляет от долей % (мас.) – для жесткоцепных, до 8-10% (мас.) – для гибкоцепных полимеров.

Условно принимают, что к среднеконцентрированным можно отнести растворы, содержащие до 0,3 объемных долей полимера, с большим содержанием полимера – к высококонцентрированным. Влияние концентрации полимеров на вязкость неразрушенной структуры растворов полимеров различной гибкости иллюстрируется рис. 14.

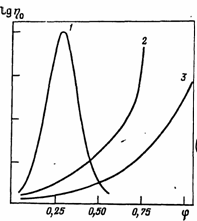
Рис. 14. Влияние концентрации полимеров (j - объемная доля полимера) на эффективную вязкость концентрированных растворов полимеров:

1 – жесткоцепные полимеры (f0<0,63); 2 – полужесткоцепные полимеры: 3 – гибкоцепные полимеры (f0>>0,63)

Возрастание h0 при увеличении концентрации происходит тем интенсивней, чем более жестки макромолекулы.

Концентрационная зависимость h0  существенно зависит от доли свободного объема системы. Согласно Фуджите-Касимото,

F(T,j*1)             1

-(lnac)-1 = f(T,j*1) + ¾¾¾¾¾ ¾¾¾¾ ,

b¢(T)              j - j*

где

h (T,j1) (1 - j*1)

ac = ¾¾¾¾¾¾¾¾¾.

h (T,j*1) (1 - j1)

Здесь h (T,j1) и h (T,j*1) – вязкость растворов с объемными долями растворителя  j1 = 1-j и j*1 при температуре Е, причем второй раствор (j*1) выбран в качестве стандартного; f(T,j*1) – доля свободного объема стандартного раствора; b¢(T) – функция взаимодействия полимера с растворителем.

Зависимость h = f(C), или h = f(j2), описывается также уравнением Келли - Бики:

lgh × BS-1 = 4lg r{j2[0,025 + 4,8×10-4(T-Tc)] +

+ (1-j2)[0,025 + aT(T-Tc¢)]},

где j2 – объемная доля полимера в растворе; BS – параметр, включающий молекулярную массу полимера; r - плотность раствора; Т – температура раствора; Тс  и Тс¢ -
температуры стеклования полимера в твердом состоянии и в растворе соответственно; aT  - температурный коэффициент свободного объема Vf .

Концентрационная зависимость вязкости растворов в первом приближении может быть описана следующими соотношениями:

по Я. Френкелю

lg h0 = A + BC1/2;

по С. Папкову

lg (lg h0) = A + BlgC,                                                                 (4)

где А и В – постоянные для данной системы полимер - растворитель; С – концентрация полимера (по массе).

Для ряда волокнообразующих полимеров (ХПВХ, ПАН, АЦ) может быть принято полулогарифмическое соотношение в области средних концентраций:

lg h0 = A + BC.                                                                          (5)

В этом случае значения постоянных А и В существенно зависят от термодинамического качества растворителя: его ухудшение обуславливает более резкое увеличение h0. Эти результаты свидетельствуют о том, что вязкость изоконцентрированных растворов тем ниже, чем лучше термодинамические качества растворителя. Очевидно, что уравнения 4 и 5 описывают соответствующие прямолинейные зависимости, а это позволяет проводить расчетную оценку вязкостных свойств при различных концентрациях полимеров.

Если размеры сегмента меньше размеров макромолекулы, то элементарные акты течения не зависят от молекулярной массы (ММ). Однако для совершения необратимого перемещения макромолекулы в целом необходимо смещение ее центра тяжести. Но чем выше ММ полимера, т. е. чем больше сегментов в макромолекуле, тем большее число согласованных движений сегментов должно произойти для перемещения ее центра тяжести и тем более высокой должна быть вязкость.

Существует две области ММ линейных полимеров, разделенных характерным для каждого полимергомологического ряда критическим значением ММ - Мкр. В обеих областях зависимость h0(М) может быть представлена степенным законом:

ì а Мa при М<Мкр

h0(М) = í                                                                                             (6)

î в Мb  при М³Мкр

Здесь а и в – индивидуальные константы полимергомологического ряда. Величина a ³ 1, b = 3,4–3,5. Типичный пример таких экспериментальных данных – зависимость для полиметиленов.

Угловые коэффициенты участков ломаной линии (значения a и b) до Мкр » 1, после Мкр » 3,5.

По достижении критической ММ изменяется комплекс свойств, присущих полимерам (вещество может быть отнесено к полимеру лишь по достижении Мкр).

По зависимости h0(М) найдены следующие значения Мкр: ПЭ – 4000; полибутадиен – 5600; полиизобутилен – 17 000; ПС – 35 000; полидиметилсилоксан – 29 000; ПВА – 22 500; ПММА – 27 500. Достижение критической молекулярной массы принято связывать с появлением в полимере пространственной сетки узлов типа зацеплений макромолекул, которые характеризуются слабыми межмолекулярными взаимодействиями и соответственно низким потенциальным барьером. Это объясняет очень слабую зависимость Мкр от температуры. Аномалия вязкости проявляется при М > Мкр и может быть связана с уменьшением плотности сетки зацеплений под влиянием сдвиговой деформации. При М > Мкр  с увеличением ММ и ростом j и t возрастает возможность разрушения сетки зацеплений – аномалия вязкости становится все более сильной. При М/Мкр » 5 у полимера обнаруживается способность переходить в высокоэластическое состояние, для которого типично существование трехмерной сетки.

Строение макромолекул существенно влияет как на h0, так и на степень аномалии вязкости. А. Чарлеби на примере полисилоксанов, подвергнутых g-облучению, показал, что вязкость разветвленных полимеров hразв меньше, чем вязкость линейных hлин с той же ММ. Снижение вязкости с увеличением разветвленности описано также для ПС, ПЭ, полиэфиров. Влияние боковых ответвлений в макромолекулах на вязкость может быть столь значительным, что отношение hлин/hразв при заданных М и Т иногда достигает нескольких десятков. Хотя вязкость разветвленного ПС понижена по сравнению с линейным ПС, темп зависимости h(М) для образцов с постоянным числом боковых цепей оказывается более высоким, чем для линейных (показатель степени b в уравнении 6 равен 4,5). Влияние разветвленности на вязкость может быть принято, если учесть, как при этом изменяется средний радиус инерции невозмущенного клубка макромолекулы. Это изменение выражается через конформационный параметр g = <S>разв/<S>лин, равный отношению среднеквадратичных радиусов инерции. Для звездообразных полимеров, например,

g = 3/р - 2/р2,                                                                             (7)

где р – число ответвлений.

Замена М величиной (g×М) в формулах 6 дает возможность правильно описать h разветвленных полимеров. Использование параметра g приводит к тому, что h = f(g×M) независима от числа ответвлений. Снижение вязкости разветвленных полимеров по сравнению с линейными той же ММ наблюдается тогда, когда длина боковых ответвлений не превосходит некоторого критического предела. В зависимости от длины боковых ответвлений отношение hлин/hразв изменяется от 1 до 10. С увеличением t и j влияние разветвленности макромолекул на hэф полимера уменьшается и при высоких скоростях сдвига  иногда может быть несущественным.